На пути к пониманию стрелок (Arrow): функции с памятью
Стрелки (тайпклассы и комбинаторы из Control.Arrow) являются замечательным обобщением понятия функции. Стрелка y a b представляет
собой некоторый процесс, принимающий значения типа a и выдающий значения типа b.
Помимо прочих мест, довольно подробная статья про стрелки есть на англоязычном Викиучебнике. Ниже я попробую пересказать её часть своими словами и подробно объяснить некоторые моменты (отсутствующие в Вики), которые сам понял не сразу.
Стрелочных комбинаторов >>>, first, &&& и прочих я коснусь в отдельной статье.
Тип Wire a b⌗
Обычные функции Haskell не обладают памятью. Функция переносит значения типа a в значения типа b. И всё. Никакого внутреннего состояния, стэйта не существует.
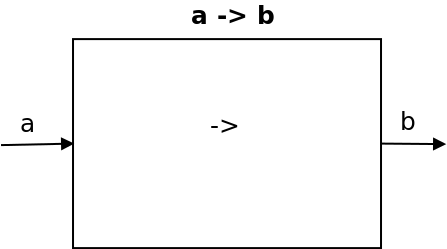
Мы можем исправить этот недостаток, построив модель процесса преобразования (его уже нельзя назвать функцией в привычном смысле этого
слова), который будет поддерживать собственный внутренний стэйт. Концептуально, процесс типа Wire a b принимает на входе a и
возвращает на выходе b. Технически, процесс типа Wire a b выдает не только результат “завёрнутого” в данный процесс преобразования из a
в b (то, с чем может справится и функция), но и процесс Wire a b – замену самому себе (быть может, слегка модифицированную).
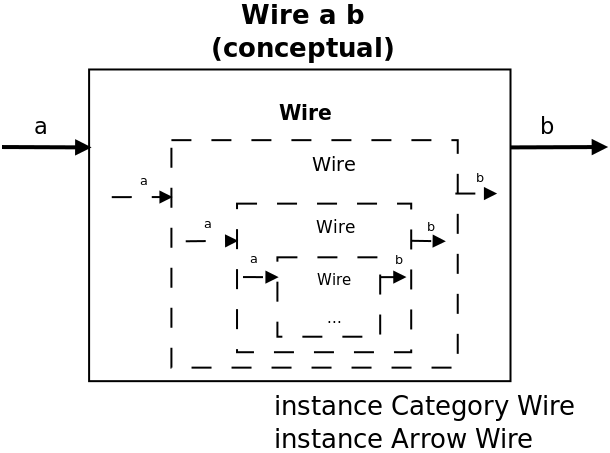
Вот так выглядит наш тип (прошу прощения за выбор названия “Wire”, а не, например, “Circuit”):
data Wire a b = Wire
{ unWire :: a -> (Wire a b, b) }
Данный тип рекурсивен (имя объявляемого типа встречается в правой части уравнения). Конструктор значений Wire a b принимает один аргумент:
функцию от a, которая возвращает новое значение Wire a b (замену) и, собственно, b, т.е. результат произведённого преобразования.
Короче говоря, для конструирования Wire (далее - “провод”) необходимо предоставить функцию от одного аргумента (вход), которая что-то
делает с этим аргументом (выход b, второй элемент пары), а также возвращает себе, функции, замену (выход Wire a b, первый элемент пары).
Разумеется, замена может быть другой, но главное - чтобы это был провод Wire a b (поскольку именно такой тип имеет “объемлющий” провод).
Вот два идентичных провода, которые считают количество символов в строке (wire1 описан с помощью лямбда-нотации, wire1' использует
для этого функцию с именем):
wire1 :: Wire String Int
wire1 = Wire $ \x -> (wire1, length x)
wire1' :: Wire String Int
wire1' = Wire wire1Func
wire1Func :: String -> (Wire String Int, Int)
wire1Func str = (fst (wire1Func str), length str)
Мы можем “запустить” вычисления в проводе напрямую (чтобы послать единичный сигнал a на входе процесса):
> :t unWire wire1 "lalala"
unWire wire1 "lalala" :: (Wire String Int, Int)
> -- хотим только результат вычисления (без вложенного провода)
> snd $ unWire wire1 "lalala"
6
или с помощью специальной функции runWire, которая рекурсивно скормит на вход процессу список, т.е. поток сигналов a (используя возвращаемые процессами копии самих себя):
runWire :: Wire a b -> [a] -> [b]
runWire _ [] = []
runWire w (a:as) = b' : runWire w' as
where
(w', b') = unWire w a
Вот пример обработки потока:
> runWire wire1 ["hello", "laalaa", "la"]
[5,6,2]
Аккумуляторная память⌗
Наши провода обладают “памятью” – рекурсивно вложенными друг в друга, может быть, слегка модифицированными в зависимости от конкретного
входного сигнала копиями себя самих. Вместе с копиями (каждая из которых, конечно же, имеет тип Wire a b) в рекурсивном “стеке вызовов”
(не смог подобрать лучшую аналогию) сожержатся и все промежуточные значения b. Значит, мы можем написать провод-аккумулятор, который
впоследствии сможет сохранять состояние между обработками сигналов из потока сигналов (функция runWire выше).
Вспомогательная функция mkAccum конструирует такой провод с аккумуляторной памятью. Для этого ей требуется собственно функция-аккумулятор
(обычная функция для “протаскивания” результата преобразования типа a в тип b и, параллельно с этим, нового значения аккумулятора
типа acc), а также стартовое значение аккумулятора. mkAccum – довольно обобщённый аккумулятор с раздельными типами для значений
аккумулятора и результатов вычисления. Уточнение mkAccum' не делает различий между “протаскиваемыми” в рекурсии новыми значениями
аккумулятора и результатами вычислений и более прост в использовании:
mkAccum :: acc -> (a -> acc -> (b, acc)) -> Wire a b
mkAccum acc0 facc = Wire $ \a ->
let
(b, acc) = facc a acc0
wab' = mkAccum acc facc
in
(wab', b)
-- less general accum
mkAccum' :: acc -> (a -> acc -> acc) -> Wire a acc
mkAccum' acc0 facc = mkAccum acc0 (\_a _acc -> (facc _a _acc, facc _a _acc))
Теперь мы можем написать провод для подсчёта текущей суммы чисел во входном потоке! total строит провод, в котором запрограммированно
стартовое значение аккумулятора 0 и использование функции +.
total :: Num a => Wire a a
total = mkAccum' 0 (+)
runWire total [0,1,2,0,0,4,2]
[0,1,3,3,3,7,9]
Процесс обладает памятью!
Category Wire⌗
Для написания программ мы хотели бы уметь удобно комбинировать вместе (последовательно выход ко входу) два и более проводов. Композиция -
центральная идея математической структуры под названием категория. Теория категорий и тайпкласс Category представлена в модуле Control.Category.
Идею ассоциативных комбинаций (композиций) абстрактных сущностей захватывает категория. Сделаем Wire экземпляром тайпкласса Category.
Единственные необходимые функции – . (точка, собственно правило композиции двух проводов) и id (нейтральный элемент композиции):
-- Функции id и . из Prelude определены по-своему в Control.Category!
import qualified Control.Category as Cat
instance Cat.Category Wire where
id = Wire $ \a -> (Cat.id, a)
(Wire wbc) . (Wire wab) = Wire $ \a ->
let (wab', b) = wab a
(wbc', c) = wbc b in
(wbc' Cat.. wab', c)
Композиция процессов Wire a b и Wire b c (у . обратный порядок) есть процесс Wire a c. Композиция процессов проводит вычисления в
каждом из них (получая b из a, а затем, наконец, c из b), а в качестве самозамены возвращает (но не выполняет) процесс-композицию
их самозамен.
Проверим с проводом wire2, который удваивает число на входе:
wire2 :: Wire Int Int
wire2 = Wire $ \x -> (wire2, x * 2)
runWire (wire2 Cat.. wire1) ["haskell", "is", "cool"]
[14,4,8]
Теперь мы можем создавать модульные программы из отдельных блоков: wn . ... . w3 . w2 . w1, где точка (.) – это композиция категорий (а не функций, как в Прелюдии).
Arrow Wire⌗
Стрелки предоставляют нам мощные возможности манипуляции потоком сигналов на пути от провода к проводу (от стрелки к стрелки). Чтобы
реализовать интерфейс тайпкласса Arrow нам нужно объяснить две вещи:
- Каким образом получить провод
Wire a bиз обыкновенной функцииa -> b. - Каким образом из (одножильного) провода
Wire a bполучить новый двухжильный (имеется в виду тьюпл) проводWire (a, d) (b, d), в котором преобразование сигнала, запрограммированное в оригинальномWire a b, применяется только лишь к первой жиле. Вторая жила в новом проводе оставлена для проброски сигнала дальше, к следующим звеньям проводной цепи.
Последний пункт, в особенности, позволяет представить всю программу в виде схемы преобразований и роутинга сигналов между звеньями, что является удобным и мощным способом создания определённого программного обеспечения. В частности, на стрелках основаны многие библиотеки функционального реактивного программирования (FRP) вроде Yampa.
Вот реализация двух важнейших функций тайплкласса Arrow для Wire:
instance Arrow Wire where
arr fab = Wire $ \a -> (arr fab, fab a)
-- first :: a b c -> a (b, d) (c, d)
first wbc = Wire $ \(b, d) ->
let (wbc', c) = unWire wbc b
in
(first wbc', (c, d))
Следует обратить внимание на рекурсию по first wbc' в комбинаторе first. Если бы функция возвратила тьюпл с first wbc, а не с wbc'
(штрихованная версия, объявленная строчкой выше), то провода, построенные на принципе самозамены слегка изменёнными копиями (в частности, наш аккумуляторный провод), перестали бы работать: в рекурсивных вызовах использовался бы один и тот-же исходный провод.
Теперь мы можем использовать синтаксис стрелок (т.н. proc-нотацию) и стрелочные комбинаторы для создания сложных схем из проводов (об этом
в следующий раз). В примере ниже провод mean2 написан в удобной proc-нотации (mean2 полностью эквивалентен mean1):
wire1A :: Wire String Int
wire1A = arr length >>> wire2
mean1 :: Fractional a => Wire a a
mean1 = (total &&& (const 1 ^>> total)) >>> arr (uncurry (/))
mean2 :: Fractional a => Wire a a
mean2 = proc value -> do
t <- total -< value
n <- total -< 1
returnA -< t / n
Результат в ghci (провод mean? вычисляет среднее значение):
> runWire wire1A ["haskell", "and", "arrows"]
[14,6,12]
> runWire mean1 [0,10,7,8]
[0.0,5.0,5.666666666666667,6.25]