Функторы в теории категорий⌗

Как известно, функтор в теории категорий определён как морфизм между двумя категориями (маппинг всех объектов одной категории в объекты другой, маппинг всех морфизмов одной категории в морфизмы другой), который сохраняет нейтральные элементы (Identity) и композицию в соответствующих категориях.

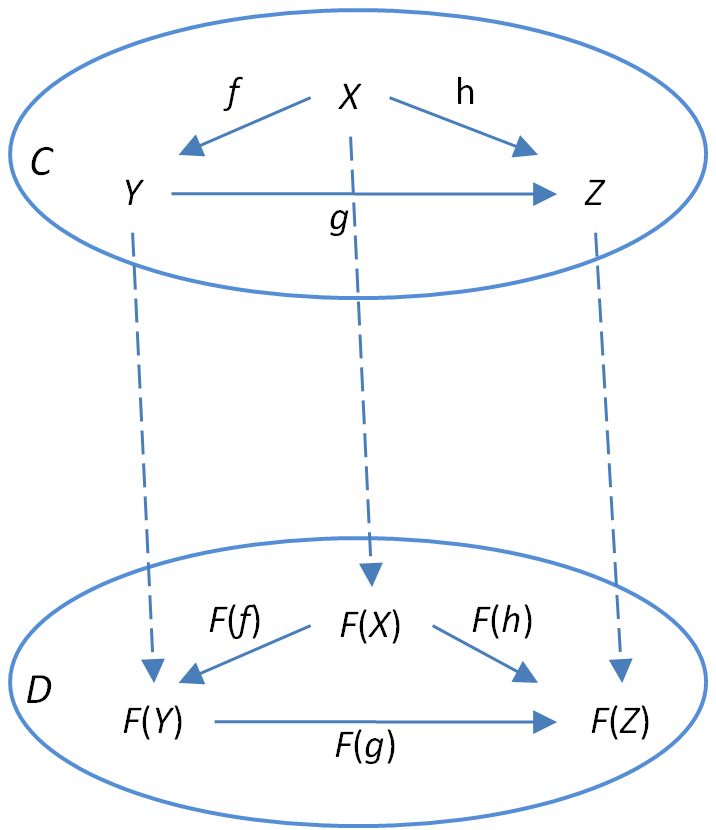
Функтор, таким образом, – более общий случай понятия гомоморфизма (групп, моноидов и т.п.), то есть отображения, сохраняющего (алгебраическую) структуру.

Функторы в философии⌗

В отличии от Множества, которое по своей природе лишено всякой структуры, любая Категория – это сама структура в чистом виде (и ничего кроме структуры). Если Категория сопоставима с нашими знаниями или моделями Мира, то Функтор представляет собой процесс осмысления (мышления в принципе), то есть отожествление, распознавание паттернов внутри некоторой объемлющей Категории (например, категории реального Мира).

Чтобы осмыслить, то есть распознать некоторую структуру внутри чего-либо, необходимо для начала создать такую структуру (модель, гипотезу, паттерн, наши ожидания, …), то есть выбрать исходную категорию C.

Мы никогда не сможем отыскать структуру там, где её нет, а значит в качестве “места для поисков” не подойдёт просто Множество, то есть Совокупность чего-либо. Для наших поисков мы используем некоторую другую Категорию, категорию D.

Функтор F : C -> D представляет собой процесс поиска, установления определённой связи между Структурами: он переносит Связи (морфизмы и композиции) из одного мира в другой. Может быть, с потерей информации (неинъективностью, то есть коллапсом нескольких связей в одну), но никогда с разрушением связей (нарушением композиции морфизмов).

Функторы в программировании⌗

Определение выше прямо так и переносится на язык Haskell: некоторый тип f – функтор, если известно как переносить морфизмы из одной категории в категорию таких типов f.

fmap :: (a -> b) -> (f a -> f b)

Строго говоря, обе категории (с морфизмами a -> b, с морфизмами f a -> f b) в случае Haskell будут одной и той же: категорией Hask с объектами - типами данных и морфизмами - функциями между типами. Это нормально, поскольку в определении функтора ничего не сказано о том, что исходная и целевая категории должны различаться. Получается, что все функторы в Haskell – технически эндофункторы.

Сохранение структуры при ассоциации морфизмов друг с другом достигается следующим требованием, ожидаемым компилятором от нашего типа:

fmap (f . g)  ==  fmap f . fmap g
fmap id  ==  id

Функтор, как и многие другие концепции в Haskell, в общем-то, представляет собой довольно абстрактную идею (как никогда близкую к чистой математике), поэтому многие программисты имеют несколько “конкретных интуиций” о том, какие же из прикладных задач могут быть решены функторами (причём довольно изящно).

Интуиция функтора как контейнера⌗

Идея функтора как контейнера, позволяющего работать с содержимым с гарантией сохранения формы контейнера.

Например, типы списков, аннотированных пар, деревьев и т.п. – это функторы. У каждого из этих типов есть своя функция fmap, показывающая как производить операции с данными внутри соответствующего контейнера:

-- Списки: рекурсивно проходим от головы до хвоста списка, применяя 
--  функцию к каждому элементу, объединяя всё в такой же контейнер []
instance Functor [] where
    fmap = map

map :: (a -> b) -> [a] -> [b]
map _ []     = []
map f (x:xs) = f x : map f xs

-- Тип "пар с первым элементом a": применяем функцию ко второму элементу,
--  сохраняя аннотацию
instance Functor ((,) a) where
    fmap f (x,y) = (x, f y)

-- Дерево, рекурсия по вершинам
instance Functor Tree where
    fmap = fmapTree
    x <$ Node _ ts = Node x (map (x <$) ts)

fmapTree :: (a -> b) -> Tree a -> Tree b
fmapTree f (Node x ts) = Node (f x) (map (fmapTree f) ts)

Контейнеры-функторы дают возможность не думать о форме контейнера и использовать “обыкновенные” функции между типами a и b внутри контейнера, хранящего тип a (на выходе, соответственно, получим такой же контейнер, хранящий уже тип b).

> :t even
even :: Integral a => a -> Bool

> fmap even [1, 2, 3, 4, 5, 2]
[False,True,False,True,False,True]

Контейнер внутри контейнера:

> :t (fmap even)
(fmap even) :: (Integral a, Functor f) => f a -> f Bool

> :t fmap (fmap even)
fmap (fmap even)
  :: (Integral a, Functor f, Functor f1) => f1 (f a) -> f1 (f Bool)

> fmap (fmap even) [("one", 1), ("two", 2), ("three", 3), ("four", 4), ("five", 5), ("two", 2)]
[("one",False),("two",True),("three",False),("four",True),("five",False),("two",True)]
it :: [([Char], Bool)]

Интуиция функтора как вычислительного контекста⌗

Например, если представлять тип Maybe a как некий вычислительный контекст, который может зафейлиться, а тип (->) r (т.е. тип функций из типа r) как контекст с окружением (environment, входными параметрами) r, то реализация следующих fmap кажется довольно логичной и обоснованной практически:

-- Если контекст уже с ошибкой (т.е. Nothing), то применять функцию не к чему;
--  иначе - применяем функцию к данным и сохраняем "незафейленность"
instance  Functor Maybe  where
    fmap _ Nothing       = Nothing
    fmap f (Just a)      = Just (f a)

-- Лифтинг функции в контекст с окружением означает прекомпозицию с результатом,
--  то есть применение функции "после получения результата в контексте"
instance Functor ((->) r) where
    fmap = (.)

Пример изменения работы вычислительного контекста с сохранением “формы” (сигнатуры, интерфейса) исходного контекста:

> let f = (even :: Int -> Bool)
f :: Int -> Bool
> let f_and_then_not = fmap (not) f
f_and_then_not :: Int -> Bool

> f 10
True
> f_and_then_not 10
False

Интуиция функтора как адаптера между категориями⌗

Если мы знаем, с какими категориями мы работаем, то интересной представляется интуиция о функторах как об “адаптерах” между категориями.

Известно, что хорошо написанные компьютерные программы имеют сильно модульную структуру. Каждый такой модуль, например библиотека, имеет чёткие правила интеграции (композиции) с остальными блоками программы, образуя своего рода интерфейсы. Очень часто за такими интерфейсами скрываются категории (модулей программы и их композиций), и отожествление или распознавание паттернов, о котором говорилось выше, одного интерфейса внутри другого является не чем иным, кроме как адаптером совместимости одного интерфеса с другим.

Например, ниже мы с лёгкостью можем использовать интерфейс списков [] внутри интерфейса моноида по сложению (моноидальной категории).

-- Адаптация библиотек мира списков для библиотек мира Sum
adapt :: Num b => [a] -> Sum b
adapt [] = mempty
adapt (x:xs) = Sum 1 <> adapt xs


-- Какой-то код для интерфейса списков
foo :: Int -> [a] -> [a]
foo n = (drop n . concat . permutations)


-- Программа (работаем в интерфейсе Sum)
prog :: Sum Int
prog =
  Sum 10 <> Sum 20 <> adapt "four" <> Sum 6 <> adapt (foo 3 [1,2,3])

Такую адаптацию ещё называют лифтингом. Трансформеры монад построены на этой идее.

Ссылки:

The functor design pattern